Bilangan kompleks adalah
bilangan yang terdiri dari 2 buah bagian, yakni: bagian nyata atau
real dan bagian khayalan atau imajiner. Bagian
nyata adalah bilangan real seperti yang kita gunakan sehari-hari, seperti: 3;
-1; 1,1; 3,14. Sementara bagian imajiner adalah bagian bilangan kompleks yang
merepresentasikan perkalian dengan identitas i (bilangan
imajiner) Apa itu bilangan imajiner?
Bilangan imajiner adalah
bilangan yang jika dikuadratkan menghasilkan -1. Dengan kata lain i = √(-1).
Karena bilangan kompleks dapat
dinyatakan sebagai 2 bagian, kita bisa tuliskan bilangan kompleks sebagai
penjumlahan dari bagian real dan bagian imajiner. Contohnya:
3 + 4i
2 + i
0 + 3i
Umumnya kita akan menuliskannya
sebagai a + bi dengan a adalah bagian bilangan real, dan b
adalah bagian bilangan imajiner.
Hampir sama dengan
bilangan-bilangan lain, bilangan kompleks juga memiliki sifat-sifat. Bilangan
kompleks tertutup terhadap operasi penumlahan, pengurangan, perkalian, dan
pembagian. Artinya, keempat operasi tersebut dapat menghasilkan bilangan
kompleks juga.
Operasi Hitung Bilangan Kompleks
Penjumlahan dua buah bilangan kompleks dinyatakan sebagai:
(a + b i) + (c + d i) = (a + c) + (b + d) i
Artinya, penjumlahan bilangan
kompleks semudah menjumlahkan setiap bagian bilangan kompleks yang sama. Jika
dilihat bagian nyata dari bilangan pertama dan kedua dijumlahkan (a + c)
kemudian bagian khayalan juga dijumlahkan terhadap sesamanya (b + d). Untuk
kasus pengurangan juga tak jauh berbeda. Namun yang harus diperhatikan adalah,
pengurangan hanya terjadi pada setiap bagian yang sama. Dengan kata lain
(a + b i) –
(c + d i) = (a – c) + (b – d) i
Kenapa menjadi (a – c) + i (b – d)
bukan (a – c) – i (b – d) atau jawaban lain? Jawabannya sederhana tanda +
mengatakan bahwa terdapat dua buah bagian bilangan yang membentuk bilangan
kompleks.
Contoh:
(3 + 5 i)
+ (2 + 2 i)
= (3 + 2) + (5 + 2) i
= 5 + 7 i
(4 + 2 i)
– (3 + 1 i)
= (4 – 3) + (2 – 1) i
= 1 + 1 i
= 1 + i
1.
Penjumlahan.
Contoh : ( 3 + 2 i ) + ( -2 + 7i ) = ................................
Jawaban :
( 3 + 2i ) + ( -2 + 7i ) = 3 + 2i – 2 + 7i = 1 + 9i.
Contoh : ( 3 + 2 i ) + ( -2 + 7i ) = ................................
Jawaban :
( 3 + 2i ) + ( -2 + 7i ) = 3 + 2i – 2 + 7i = 1 + 9i.
2.
Pengurangan.
Contoh : ( 2 - 3i ) - ( 8 - 2i ) = ......................................
Jawaban :
( 2 - 3i ) - ( 8 - 2 i ) = 2 – 3i - 8 + 2i = -6 – i
Contoh : ( 2 - 3i ) - ( 8 - 2i ) = ......................................
Jawaban :
( 2 - 3i ) - ( 8 - 2 i ) = 2 – 3i - 8 + 2i = -6 – i
Perkalian
Aturan perkalian pada bilangan kompleks sebenarnya cukup sederhana.
(a + b i) x (c + d i)
=> a x c + a x d i + b x c i + b x d x i x i
=> (a x c – b x d) + (a x d + b x c) i
sehingga
(a + b i) x (c + d i) = (a x c – b x d) + (a x d + b x c) i
Ingat lagi bahwa i adalah akar kuadrat dari -i dengan demikian i kuadrat akan menghasilkan -1 sehingga b x d x i x i akan menghasilkan – b x d. Bilangan ini adalah bilangan real karena sudah tak mengandung i lagi.
Contoh:
(3 + i) x (2 + 3 i)
= (3 x 2 – 1 x 3) + (3 x 3 + 1 x 2) i
= 3 + 11 i
3. Perkalian .
Contoh : ( 3 + 4i )( 2 – 5i ) = ..........................................
Jawaban :
( 3 + 4i )( 2 – 5i ) = 6 – 15i + 8i - 20i2
Ubah i2 = -1 , maka :
( 3 + 4i )( 2 – 5i ) = 6 – 15i + 8i + 20 = 26 - 7i.
Pembagian
Pembagian bilangan kompleks boleh dibilang sedikit lebih njlimet (baca: rumit). Ide dasarnya adalah kita membuat penyebut (bilangan yang ada di bagian bawah dalam pecahan) menjadi sederhana. Langsung saja kita ke contoh:
(a + b i) / (c + d i)
Misal (a + b i) dibagi dengan (c
+ d i). Kita perlu membuat c + d i menjadi sederhana. Kita tahu bahwa (x + y)
dikali dengan (x – y) akan menghasilkan (x*x – y*y). Kita akan memanfaatkan
sifat ini. Tapi kalau begitu, supaya adil bagian pembilang juga harus dikalikan
dengan nilai yang sama. Maka kita dapatkan:
( (a + b i) x
(c – d i) ) / ( (c + d i) x (c-d i) )
=> ( (a + b i) x (c – d i) ) / ( c^2 + d^2)
=> ( (a x c + b x d) + ( – a x d + b x c) i ) / (
c^2 + d^2)
Perhatikan, tanda ^ berarti
pangkat. C^2 berarti c pangkat 2 atau c kuadrat.
Contoh:
(2 + 3 i) /
(1 + 2 i)
= ( (2 + 3 i) x (1 – 2 i) ) / ( (1 + 2 i) x (1 – 2
i) )
= ( (2 x 1 + 3 x 2) + ( -2 x 2 + 3 x 1) i )
/ ( 1^2 + 2^2 )
= ( 8 – i ) / 5
Contoh Soal pembagian :

= ....
Jawab:
Lihat bagian penyebut, yaitu 3+4i. Maka, sekawan/konjugatnya adalah 3-4i. Kalikan bilangan konjugat ini di pembilang dan penyebut.. (lihat langkah di bawah).
 =
= 


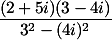






0 comments:
Post a Comment