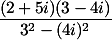Rumus Mudah Trigonometri

 

sumber : twitter.com

   Trigonometri (dari bahasa Yunani trigonon = "tiga sudut" dan metron = "mengukur") adalah sebuah cabang matematika yang mempelajari hubungan yang meliputi panjang dan sudut segitiga. Trigonometri mudah dikaitkan dalam bidang segitiga siku-siku (dengan hasil jumlah besar kedua sudut lancip sama dengan besar sudut siku-siku). Peranan untuk selain segitiga siku-siku juga ada. Sejak segitiga yang bukan siku-siku dapat dibagi menjadi dua segitiga siku-siku, banyak masalah yang dapat diatasi dengan penghitungan segitiga siku-siku. Karena itu, sebagian besar penggunaan trigonometri berhubungan dengan segitiga siku-siku.

Continue reading →

Tujuh Rumus Matematika Dasar Yang Penting dan Perlu di Ingat

Matematika (dari bahasa Yunani: μαθημα - mathēma, "pengetahuan, pemikiran, pembelajaran") adalah ilmu yang mempelajari hal-hal seperti besaran, struktur, ruang, dan perubahan. (https://id.wikipedia.org/wiki/Matematik)

Matematika sendiri sering kali menjadi musuh bagi murid-murid yang sedang mempelajarinya karena memerlukan effort yang lebih untuk menyelesaikan tiap soalnya. Padahal matematika sendiri adalah ilmu yang mempersingkat suatu pekerjaan, sebagai contoh untuk menghitung sesuatu volume benda kita dapat mengaplikasikan rumus volume yang ada agar dapat dikerjakan dengan tepat dan cepat. Berikut adalah tujuh rumus dasar matematika yang perlu diingat :

1. Rumus Volume Bangun Ruang

Nama Bangun Ruang	Rumus Volume
Tabung	V = phi r² x t
Prima tegak segitiga	V = Luas alas x Tinggi

2. Rumus Skala dan Jarak Peta

Rumus Skala	= Jarak Pada Gambar (Peta) / Jarak Sebenarnya
Rumus Jarak Pada Gambar	= Jarak Sebenarnya x Skala
Rumus Jarak Sebenarnya	= Jarak Pada Gambar (Peta) / Skala

3. Rumus Menghitung Luas Bangun Datar

Bangun Datar	Rumus Luas
Bangun Datar Persegi	L = sisi x sisi = s²
Bangun Datar Segitiga	L = ½ alas x tinggi
Bangun Datar Lingkaran	L = phi x r²
Bangun Datar Trapesium	L = ½ t × (a+b)
Bangun Datar Layang – Layang	L = ½ x d1 x d2
Bangun Datar Jajar Genjang	L = Alas x Tinggi
Bangun Datar Belah Ketupat	L = ½ x d1 x d2
Bangun Datar Persegi Panjang	L = Panjang x Lebar

4. Rumus Operasi Bilangan Bulat

a. Sifat Komutatif Penjumlahan, Rumus Bentuk Umum : a + b = b + a

Contohnya : 2 + 4 = 4 + 2 = 6 atau 5 + 10 = 10 + 5 = 15

b. Sifat komutatif Perkalian, Rumus Bentuk Umum : a x b = b x a

Contohnya : 3 x 5 = 5 x 3 = 15 atau 10 x 2 = 2 x 10 = 20

c. Sifat Distributif Perkalian terhadap Penjumlahan

Rumus Umumnya : a x (b + c) = (a x b) + (a x c)

Contohnya :

2 x (5 + 10)	= 2 x 5 + 2 x 10
	= 10 + 20
	= 30

d. Sifat Distributif Perkalian terhadap Pengurangan

Rumus Umumnya : a x (b – c) = (a x b) – (a x c)

Contohnya :

2 x (10 – 5)	= 2 x 10 – 2 x 5
	= 20 + 10
	= 10

5. Rumus Operasi Hitung Bilangan Campuran

Didalam Rumus Operasi Hitung Bilangan terdapat Dua Ketentuan antara lain yang pertama jika terdapat kurung () maka kerjakan yg didalam kurung terlebih dahulu dan ketentuan yang kedua adalah jika tidak ada Kurung () maka perkalian dan pembagian didahulukan terlebih dahulu dari dari penjumlahan dan pengurangan.

Contoh :

= 7000 – 40 x 100 : 4 + 200 = 7000 – 1000 + 200 = 6200

Atau

= 1000 : 10 x 2 – (200 –  50) = 1000 : 10 x 2 – 150 = 100 x 2 – 150 = 200 – 150 = 50

6. Rumus FPB dan KPK Dua Bilangan

a. Cara Menentukan FPB (Faktor Persekutuan Terbesar) Dua Bilang antara lain Cari Faktor pada masing2 bilangan tersebut, tentukan Faktor Persekutuan dari kedua bilangan tersebut dan Kalikan Faktor Persekutuan (Faktor yg sama) yang mempunyai pangkat yang paling kecil.

Contohnya :

27	= 3³
18	= 2 x 3²

Faktor yang sama dari FPB Dua Bilangan tersebut ialah 3, dan yang berpangkat yang paling kecil adalah 3² = 9

b. Cara Menentukan KPK (Kelipatan Persekutuan Terkecil) Dua Bilangan antara lain Cari Faktor Prima dari Masing – Masing Bilangan tersebut, kalikan semua faktor dan faktor yg sama tersebut dipilih pangkat yang paling tinggi.

Contohnya : Nilai KPK 12 dan 15

12	= 2² x 3
15	= 3 x 5

 Nilai KPK Dua Bilangan diatas : 2² x 3 x 5 = 50

7. Rumus Matematika SD Volume dan Waktu

Satuan Waktu

Satu Menit	= 60 Detik
Satu Jam	= 60 Menit
Satu Hari	= 24 Jam
Satu Minggu	= 7 Hari
Satu Bulan	= 30 Hari / 31 Hari
Satu Bulan	= 4 Minggu
Satu Tahun	= 52 Minggu
Satu Tahun	= 12 Bulan
Satu Windu	= 8 Tahun
Satu Dekade	= 10 Tahun
Satu Dasawarsa	= 10 Tahun
Satu Abad	= 100 Tahun
Satu Milenium	= 1000 Tahun

Continue reading →

Bilangan kompleks

Bilangan kompleks adalah bilangan yang terdiri dari 2 buah bagian, yakni: bagian nyata atau real dan bagian khayalan atau imajiner. Bagian nyata adalah bilangan real seperti yang kita gunakan sehari-hari, seperti: 3; -1; 1,1; 3,14. Sementara bagian imajiner adalah bagian bilangan kompleks yang merepresentasikan perkalian dengan identitas i (bilangan imajiner) Apa itu bilangan imajiner?

Bilangan imajiner adalah bilangan yang jika dikuadratkan menghasilkan -1. Dengan kata lain i = √(-1).

Karena bilangan kompleks dapat dinyatakan sebagai 2 bagian, kita bisa tuliskan bilangan kompleks sebagai penjumlahan dari bagian real dan bagian imajiner. Contohnya:

3 + 4i

2 + i

0 + 3i

Umumnya kita akan menuliskannya sebagai a + bi dengan a adalah bagian bilangan real, dan b adalah bagian bilangan imajiner.

Hampir sama dengan bilangan-bilangan lain, bilangan kompleks juga memiliki sifat-sifat. Bilangan kompleks tertutup terhadap operasi penumlahan, pengurangan, perkalian, dan pembagian. Artinya, keempat operasi tersebut dapat menghasilkan bilangan kompleks juga.

  

Operasi Hitung Bilangan Kompleks

Penjumlahan dan Pengurangan
Penjumlahan dua buah bilangan kompleks dinyatakan sebagai:
(a + b i) + (c + d i) = (a + c) + (b + d) i

Artinya, penjumlahan bilangan kompleks semudah menjumlahkan setiap bagian bilangan kompleks yang sama. Jika dilihat bagian nyata dari bilangan pertama dan kedua dijumlahkan (a + c) kemudian bagian khayalan juga dijumlahkan terhadap sesamanya (b + d). Untuk kasus pengurangan juga tak jauh berbeda. Namun yang harus diperhatikan adalah, pengurangan hanya terjadi pada setiap bagian yang sama. Dengan kata lain

(a + b i) – (c + d i) = (a – c) + (b – d) i

Kenapa menjadi (a – c) + i (b – d) bukan (a – c) – i (b – d) atau jawaban lain? Jawabannya sederhana tanda + mengatakan bahwa terdapat dua buah bagian bilangan yang membentuk bilangan kompleks.

Contoh:

(3 + 5 i) + (2 + 2 i)

= (3 + 2) + (5 + 2) i

= 5 + 7 i

(4 + 2 i) – (3 + 1 i)

= (4 – 3) + (2 – 1) i

= 1 +  1 i

= 1 + i

1.      Penjumlahan.
Contoh : ( 3 + 2 i ) + ( -2 + 7i ) = ................................
Jawaban :
( 3 + 2i ) + ( -2 + 7i ) = 3 + 2i – 2 + 7i = 1 + 9i.

2.      Pengurangan.
Contoh : ( 2 - 3i ) - ( 8 - 2i ) = ......................................
Jawaban :
( 2 - 3i ) - ( 8 - 2 i ) = 2 – 3i - 8 + 2i = -6 – i

Perkalian
Aturan perkalian pada bilangan kompleks sebenarnya cukup sederhana.
(a + b i) x (c + d i)
=> a x c + a x d i + b x c i + b x d x i x i
=> (a x c – b x d) + (a x d + b x c) i
sehingga
(a + b i) x (c + d i) = (a x c – b x d) + (a x d + b x c) i
Ingat lagi bahwa i adalah akar kuadrat dari -i dengan demikian i kuadrat akan menghasilkan -1 sehingga b x d x i x i akan menghasilkan – b x d. Bilangan ini adalah bilangan real karena sudah tak mengandung i lagi.
Contoh:
(3 + i) x (2 + 3 i)
= (3 x 2 – 1 x 3) + (3 x 3 + 1 x 2) i
= 3 + 11  i
3. Perkalian .
Contoh : ( 3 + 4i )( 2 – 5i ) = ..........................................
Jawaban :
( 3 + 4i )( 2 – 5i ) = 6 – 15i + 8i - 20i2
Ubah i2 = -1 , maka :
( 3 + 4i )( 2 – 5i ) = 6 – 15i + 8i + 20 = 26 - 7i.

Pembagian
Pembagian bilangan kompleks boleh dibilang sedikit lebih njlimet (baca: rumit). Ide dasarnya adalah kita membuat penyebut (bilangan yang ada di bagian bawah dalam pecahan) menjadi sederhana. Langsung saja kita ke contoh:
(a + b i) / (c + d i)

Misal (a + b i) dibagi dengan (c + d i). Kita perlu membuat c + d i menjadi sederhana. Kita tahu bahwa (x + y) dikali dengan (x – y) akan menghasilkan (x*x – y*y). Kita akan memanfaatkan sifat ini. Tapi kalau begitu, supaya adil bagian pembilang juga harus dikalikan dengan nilai yang sama. Maka kita dapatkan:

( (a + b i) x (c – d i) ) / ( (c + d i) x (c-d i) )

=> ( (a + b i) x (c – d i) ) / ( c^2 + d^2)

=> ( (a x c + b x d) + ( – a x d + b x c) i ) / ( c^2 + d^2)

Perhatikan, tanda ^ berarti pangkat. C^2 berarti c pangkat 2 atau c kuadrat.

Contoh:

(2 + 3 i) / (1 + 2 i)

= ( (2 + 3 i) x (1 – 2 i) ) / ( (1 + 2 i) x (1 – 2 i) )

= ( (2 x 1 + 3 x 2) + ( -2 x 2 + 3 x 1) i )  /  ( 1^2 + 2^2 )

= ( 8 – i ) / 5

Contoh Soal pembagian :




= ....


Jawab:
Lihat bagian penyebut, yaitu 3+4i. Maka, sekawan/konjugatnya adalah 3-4i. Kalikan bilangan konjugat ini di pembilang dan penyebut.. (lihat langkah di bawah).

= 

                     

                       

                        

                         

Continue reading →